Гномон
Обычный шест, вертикально воткнутый в землю стал первым астрономическим прибором. Что может быть проще? Однако и с его помощью можно сделать очень многое!
Гномон предназначен для определения положения Солнца по его тени. Да, это всего лишь вертикальный шест на горизонтальной площадке. (Надеюсь, не нужно объяснять, как его изготовить?  ) Только учтите, что для получения достаточно точных результатов гномон должен быть выставлен по отвесу и иметь высоту хотя бы около метра или выше.
) Только учтите, что для получения достаточно точных результатов гномон должен быть выставлен по отвесу и иметь высоту хотя бы около метра или выше.
Представим себя на месте древних астрономов или потерпевших крушение моряков на необитаемом острове и посмотрим, что же можно сделать с гномоном. Конечно, определить высоту Солнца - для этого достаточно найти арктангенс отношения длины тени к высоте гномона... Стоп! Арктангенс без калькулятора (да и то не всякого) или без таблиц Брадиса мы не посчитаем. А ведь мы пытаемся понять, как действовали древние астрономы - калькуляторов у них точно не было. Вообще, в древности обычно углы измеряли в долях окружности, но мы все же будем пользоваться привычными нам градусами. Для этого отложим высоту гномона на земле перпендикулярно линии тени - мы построили точную копию исходного треугольника. Искомый угол (прилежащий к концу тени гномона) можно измерить непосредственно транспортиром, ну а если вдруг на нашем необитаемом острове не нашлось этого полезнейшего инструмента  , придется проделать некоторые геометрические построения. Построим окружность с центром в точке конца тени гномона, откладывая радиус окружности по ее дуге, разобьем ее на сегменты по 60 градусов. Последовательно построив биссектрисы углов, мы легко получим метки 30, а затем 15 градусов. Можно так действовать и дальше, однако полученные углы будут иметь дробную величину, что не очень удобно. Для наших же целей достаточно "на глаз" разделить полученные 15-градусные дуги на 5-градусные части (к сожалению, деление угла или дуги на 3 равные части нельзя выполнить построениями) и затем так же "на глаз" разметить их на градусные деления - точность должна получиться при некоторой аккуратности не хуже 1/2 градуса.
, придется проделать некоторые геометрические построения. Построим окружность с центром в точке конца тени гномона, откладывая радиус окружности по ее дуге, разобьем ее на сегменты по 60 градусов. Последовательно построив биссектрисы углов, мы легко получим метки 30, а затем 15 градусов. Можно так действовать и дальше, однако полученные углы будут иметь дробную величину, что не очень удобно. Для наших же целей достаточно "на глаз" разделить полученные 15-градусные дуги на 5-градусные части (к сожалению, деление угла или дуги на 3 равные части нельзя выполнить построениями) и затем так же "на глаз" разметить их на градусные деления - точность должна получиться при некоторой аккуратности не хуже 1/2 градуса.
Можно поступить иначе - с помощью циркуля или какого-либо предмета, играющего роль "эталона длины" отмерим радиус будущей окружности в 57.3 единицы, тогда отложенные по дуге единичные отрезки будут соответствовать величине угла в 1 градус. Комбинируя эти способы, можно получить достаточно точный "транспортир".
Другая важнейшая задача, легко решаемая с помощью гномона - точное определение сторон горизонта и момента полдня. Для этого нужно за несколько часов до полудня построить окружность с центром в основании гномона и проходящую через конец тени. Наблюдая за движением тени, мы заметим, что она укорачивается, край тени описывает кривую, приближаясь к основанию гномона, а после полудня начинает удлиняться и спустя пару часов достигает окружности - нам необходимо отметить точку, в которой край тени пересечет ее. Середина отрезка между отмеченными на окружности точками и даст направление полуденной линии - построим ее, соединив эту точку с основанием гномона.
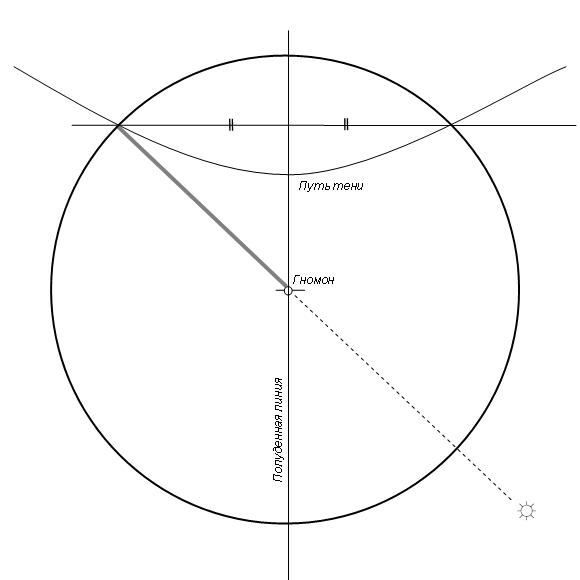
Строго говоря, этот способ имеет некоторую погрешность - дело в том, что Солнце в течение дня успевает немного сместиться по склонению (высота Солнца в полдень меняется изо дня в день) и построенная нами хорда будет несколько смещенной. Эта ошибка будет максимальна вблизи равноденствий (21 марта и 22 сентября), когда склонение Солнца изменяется особенно быстро, но и тогда она в средних широтах не превышает 1/2 градуса. Вблизи же солнцестояний (22 июня и 21 декабря) или в экваториальных широтах ошибки не будет вовсе. Мы пренебрежем этой ошибкой, так как она меньше точности наших наблюдений.
Кстати, подобную задачу решали герои Жюля Верна в романе "Таинственный остров" (глава XIII) - сравним?
Днем 2 апреля Сайрес Смит решил определить положение острова относительно стран света.
Накануне он точно установил, сделав поправку на преломление, в котором часу солнце скрылось за горизонтом.
Утром инженер с неменьшей точностью отметил время восхода солнца. Между закатом и восходом прошло двенадцать часов двадцать четыре минуты. Следовательно, рассуждал инженер, в этот день солнце через шесть часов двенадцать минут после восхода пересечет меридиан, и точка пересечения будет на севере.
В указанное время Сайрес тщательно отметил эту точку и, проведя мысленно кривую между солнцем и двумя деревьями, которые должны были служить опорными пунктами, получил постоянный меридиан для дальнейших вычислений.
Мы видим, что инженер действовал совершенно иначе. Обратите внимание, что Сайрес Смит определял продолжительность ночи непосредственно перед днем наблюдений - если бы он измерил продолжительность дня накануне, то ошибка, вызванная изменением продолжительности дня, была бы заметно больше. Что ж, в принципе этот способ тоже пригоден, однако на практике он имеет несколько недостатков:
- момент восхода и захода можно точно определить только над поверхностью моря, к тому же облачность и дымка очень часто не дают наблюдать Солнце у горизонта;
- нужны часы;
- атмосферная рефракция непостоянна, у горизонта ее случайные изменения максимальны и приводят к наибольшим ошибкам. Кстати, влияние рефракции при тех же условиях наблюдения одинаково при восходе и заходе и при определении момента полудня поправку вводить не нужно было, да ее и невозможно рассчитать, не зная хотя бы приблизительно широты точки наблюдения, температуры и давления воздуха.
- данный способ менее точен, в более высоких широтах весной и осенью ошибка из-за изменения продолжительности дня может быть слишком велика.
Ну и, наконец, в этом описании допущена грубая ошибка - в апреле в южном полушарии ночь длиннее дня и если между заходом и восходом прошло 12 часов 24 минуты, то продолжительность дня составит 11 часов 36 минут и полдень наступит через 5 часов 48 минут после восхода.  ( по материалам http://astroexperiment.ru/ )
( по материалам http://astroexperiment.ru/ )