О пользе ошибок

В прошлый раз мы познакомились с тем, как Аристарх вычислил размеры Солнца и Луны и расстояния до них. На самом деле всё было несколько сложнее. Геометрия только формировалась, и многие привычные для нас, ещё с восьмого класса школы, вещи были в то время совсем не очевидны. Аристарху потребовалось написать целую книгу, чтобы изложить то, что мы изложили на трёх страницах. И с экспериментальными измерениями тоже всё было непросто. Во-первых, Аристарх ошибся с измерением диаметра земной тени во время лунного затмения, получив отношение , вместо . Кроме того, он, вроде бы, исходил из неверного значения угла  - углового диаметра Солнца, считая его равным . Но эта версия спорная: Архимед в своём трактате "Псаммит" пишет, что, напротив, Аристарх пользовался почти правильным значением в . Однако, самая ужасная ошибка произошла на первом шаге, при вычислении параметра - отношения расстояний от Земли до Солнца и до Луны. Вместо у Аристарха получилось . Как можно было ошибиться более, чем в 20 раз ? Обратимся еще раз к шагу 1, рис 3. Для того, чтобы найти отношение Аристарх измерил угол , и тогда  . Например, если угол  был бы равен , то мы получили бы , и Солнце было бы вдвое дальше от Земли, чем Луна. Но результат измерения оказался неожиданным: угол получался почти прямым. Это означало, что катет во много раз превосходит . У Аристарха получилось , и тогда (напомним, что все вычисления у нас - приближённые). Истинное значение угла  , и  . Так погрешность измерения менее, чем в , привела к ошибке в  раз ! Завершив вычисления, Аристарх приходит к выводу, что радиус Солнца равен радиусов Земли (вместо ).

Ошибки были неизбежны, учитывая несовершенные измерительные приборы того времени. Важнее то, что метод оказался правильным. Вскоре (по историческим меркам, т.е., примерно через 100 лет) выдающийся астроном античности Гиппарх (190 - ок. 120 до н. э.) устранит все неточности и, следуя методу Аристарха, вычислит правильные размеры Солнца и Луны. Возможно, ошибка Аристарха оказалась в результате даже полезной. До него господствовало мнение, что Солнце и Луна либо вовсе имеют одинаковые размеры (как и кажется земному налюдателю), либо отличаются несильно. Даже отличие в раз удивило современников. Поэтому, не исключено, что, найди Аристарх правильное отношение  , в это никто бы не поверил, а может быть, и сам учёный отказался бы от своего метода, сочтя результат несуразным. Известный принцип гласит, что геометрия - это искусство хорошо рассуждать на плохо выполненных чертежах. Перефразируя, можно сказать, что наука в целом - это искусство делать верные выводы из неточных, или даже ошибочных, наблюдений. И Аристарх такой вывод сделал ! За 17 веков до Коперника он понял, что в центре мира находится не Земля, а Солнце. Так впервые появилась гелиоцентрическая модель и понятие Солнечной системы.

  Что в центре ?

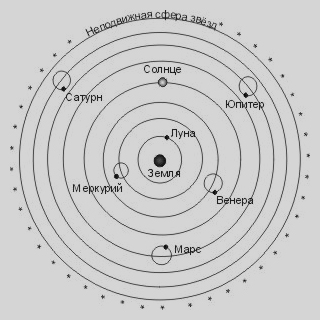
Господствовавшее в Древнем Мире представление об устройстве Вселенной, знакомое нам по урокам истории, заключалось в том, что в центре мира - неподвижная Земля, вокруг неё по круговым орбитам вращаются 7 планет, включая Луну и Солнце (которое тоже считалось планетой). Завершается все небесной сферой с прикреплёнными к ней звёздами. Сфера вращается вокруг Земли, делая полный оборот за 24 часа. Со временем в эту модель многократно вносились исправления. Так, стали считать, что небесная сфера неподвижна, а Земля вращается вокруг своей оси. Затем стали исправлять траектории движения планет: круги заменили циклоидами, т.е., линиями, которые описывают точки окружности при её движении по другой окружности (об этих замечательных линиях можно прочитать в книгах Г.Н.Бермана "Циклоида", А.И.Маркушевича "Замечательные кривые", а также в "Кванте": статья С.Верова "Тайны циклоиды" N8, 1975, и статья С.Г.Гиндикина "Звездный век циклоиды", N6,1985). Циклоиды лучше согласовывались с результатами наблюдений, в частности, объясняли "попятные" движения планет. Это - геоцентрическая система мира, в центре которой - Земля ("гео"). Во II в. н.э. она приняла окончательный вид в книге "Альмагест" Клавдия Птолемея (87-165 н.э.), выдающегося греческого астронома, однофамильца египетских царей. Со временем некоторые циклоиды усложнялись, добавлялись всё новые промежуточные окружности. Но в целом система Птолемея господствовала около полутора тысячелетий, до XVI века, до открытий Коперника и Кеплера. Поначалу геоцентрической модели придерживался и Аристарх. Однако, вычислив, что радиус Солнца в  раз больше радиуса Земли, он задал простой вопрос: почему такое большое Солнце должно вращаться вокруг такой маленькой Земли ? Ведь если радиус Солнца больше в  раз, то его объём больше почти в  раз ! Значит, в центре мира должно находиться Солнце. Вокруг него вращаются 6 планет, включая Землю.⁴ А седьмая планета, Луна, вращается вокруг Земли. Так впервые появилась гелиоцентрическая система мира ("гелиос" - Солнце). Уже сам Аристарх отмечал, что такая модель лучше объясняет видимое движение планет по круговым орбитам, лучше согласуется с результатами наблюдений. Но её не приняли ни учёные, ни официальные власти. Аристарх был обвинён в безбожии и подвергся преследованиям. Из всех астрономов античности, только Селевк стал сторонником новой модели. Больше её не принял никто, по крайней мере, у историков нет твёрдых сведений на этот счёт. Даже Архимед и Гиппарх, почитавшие Аристарха и развившие многие его идеи, не решились поставить Солнце в центр мира. Почему ?

 

Почему мир не принял гелиоцентрической системы ?

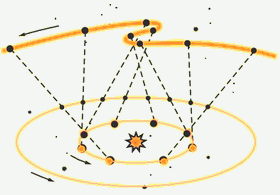
Как же получилось, что в течении 17 веков учёные не принимали простой и логичной системы мира, предложенной Аристархом ? И это несмотря на то, что официально признанная геоцентрическая система Птолемея часто давала сбои, не согласуясь с результатами наблюдений за планетами и за звёздами. Приходилось добавлять всё новые окружности (так называемые, вложенные циклы) для "правильного" описания движения планет. Самого Птолемея трудности не пугали, он писал: "К чему удивляться сложному движению небесных тел, если их сущность нам неизвестна ?" Однако, уже к XIII веку этих окружностей накопилось 75 ! Модель стала столь громоздкой, что начали раздаваться осторожные возражения: неужели мир в самом деле устроен так сложно ?

Широко известен случай с Альфонсом X (1226-1284), королем Кастильи и Леона, государства, занимавшего часть современной Испании. Он, покровитель наук и искусств, собравший при своём дворе пятьдесят лучших астрономов мира, на одной из научных бесед обмолвился, что "если бы при сотворении мира Господь оказал мне честь и спросил моего совета, многое было бы устроено проще." Подобная дерзость не прощалась даже королям: Альфонс был низложен и отправлен в монастырь. Но сомнения остались. Часть из них можно было бы разрешить, поставив Солнце в центр Вселенной и приняв систему Аристарха. Его труды были хорошо известны. Однако, ещё много веков никто из учёных не решался на такой шаг. Причины были не только в страхе перед властями и официальной церковью, которая считала теорию Птолемея единственно верной. И не только в инертности человеческого мышления: не так-то просто признать, что наша Земля - не центр мира, а лишь рядовая планета. Всё-таки, для настоящего учёного ни страх ни стереотипы - не препятствия на пути к истине. Гелиоцентическая система отвергалась по вполне научным, можно даже сказать, геометрическим причинам. Если допустить, что Земля вращается вокруг Солнца, то, её траектория - окружность с радиусом равным расстоянию от Земли до Солнца. Как мы знаем, это расстояние равно 23455 радиусов Земли, т.е., более 150 миллионов километров. Значит, Земля в течение полугода перемещается на 300 миллионов километров. Гигантская величина ! Но картина звёздного неба для земного наблюдателя при этом остаётся такой же. Земля то приближается, то удаляется от звёзд на 300 миллионов километров, но ни видимые расстояния между звёздами (например, форма созвездий), ни их яркость не меняются. Это означает, что расстояния до звёзд должны быть ещё в несколько тысяч раз больше. То есть, небесная сфера должна иметь совершенно невообразимые размеры ! Это, между прочим, осознавал и сам Аристарх, который писал в своей книге: "Объём сферы неподвижных звёзд во столько раз больше объёма сферы с радиусом Земля-Солнце, во сколько раз объём последней больше объёма земного шара". Т.е., по Аристарху выходило, что расстояния до звёзд равно , это более 3.5 триллионов километров (в реальности расстояние от Солнца до ближайшей звезды ещё примерно в 11 раз больше. В модели, которую мы представили в самом начале, когда расстояние от Земли до Солнца равно 10 м., расстояние до ближайшей звезды равно ... 2700 километров !). Вместо компактного и уютного мира, в центре которого находится Земля, и который помещается внутри относительно небольшой небесной сферы, Аристарх нарисовал бездну. И эта бездна испугала всех.        (В.Ю. Протасов
Московский Государственный Университет, Механико-математический факультет, Воробьевы Горы, Москва, 119992, e-mail: Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра.)