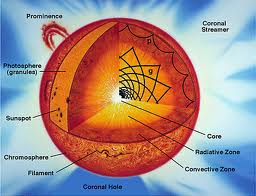
Что мы видим?

Если измерить доплеровские скорости в любой момент времени в точках видимого диска Солнца, то обнаружится весьма сложная картина повсеместных движения вещества. Продолжая наблюдения за доплеровской скоростью в выбранной малой области, можно предположить, что они квазипериодические, хотя обнаружить какие-то длительные закономерности не удается. Амплитуда скорости существенно зависит от выбранного размера области наблюдения. Если размер поля зрения около секунды, то доминирующими будут движения вещества в гранулах, которые обычно связывают с конвективным перемешиванием. Амплитуда скорости таких движений порядка 1-2 км/сек, и они преобладают в горизонтальном направлении - вещество "растекается" после выброса из конвективной зоны. Еще более важной чертой этих движений является их случайный характер - выброс и движения вещества в одной грануле никак не связаны с движениями в другой, и с последующими выбросами. Естественно ожидать, что при увеличении поля зрения (то есть при усреднении скорости по полю зрения на диске Солнца) суммарная амплитуда случайных несвязанных сигналов должна быстро уменьшаться, одновременно теряя всякие признаки периодичности.

Предметом исследования в гелиосейсмологии являются движения принципиально другого характера - а именно волновые колебания. Отличительной особенностью волны является ее периодическое поведение как во времени, так и в пространстве. Физически волна представляет собой возмущение равновесного состояния, возникшее в некоторой точке пространства и вызывающее через какое-то время отклик в соседних точках. Скорость распространения возмущения является принципиальным свойством среды, где распространяется волна, и не зависит от характера возмущения (последнее утверждение справедливо для линейных колебаний, которые обычно связывают с волнами относительно малой амплитуды).

Для выделения именно волновых движений на фоне конвективных, нужно анализировать поле скоростей в течение длительного времени и сразу во многих точках видимого диска. Только так, после анализа подобия движений в разнесенных точках и учета запаздывания волн, можно выделить волновые возмущения.

Амплитуда волновых движений почти всегда меньше, чем случайных грануляционных. Для характерных масштабов волн, видимых под углом в одну секунду, она составляет около 0.5 км/сек. С увеличением размера наблюдаемой области, амплитуда спадает, но не так, как можно было бы ожидать для суммы случайных движений. Интересно отметить, что даже если увеличить поле зрения до размеров всего видимого диска (наблюдать Солнце как звезду), волновые движения проявляют вполне измеримую амплитуду (несколько м/с), но сохраняют периодических характер, что отличает их от суммы множества случайных конвективных скоростей.

Главной характеристикой волновых движений является период P или частота ν =1/P. На Солнце наблюдаются колебания с периодами от 3 до 15 минут. Исторически первыми открыты колебания с периодом около пяти минут, что и объясняет название - пятиминутные колебания. В окрестности пяти минут мощность колебаний максимальна, хотя максимум достаточно широкий. Наблюдая волны на диске Солнца, можно измерить горизонтальную длину волны, и диапазон наблюдаемых длин волн покрывает все доступные размеры - от предельно коротких волн, которые только можно наблюдать (порядка 0.1''), до волн, с длиной, соизмеримой с полной окружностью Солнца. Волны могут распространяться в любом направлении по диску Солнца, и для описания их движения используют две горизонтальные длины волны - вдоль двух выбранных направлений - λ_x и λ_y и измеряют двумерную картину волнового поля.

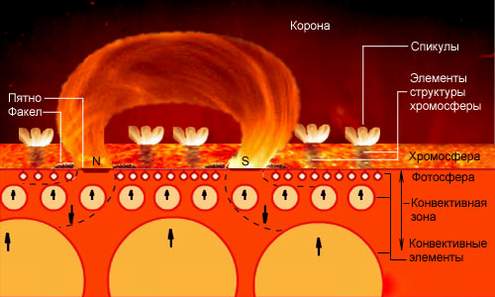
Что измеряют в гелиосейсмологии?

При таком изобилии возможных периодов и длин волн может показаться, что суммарное колебание будет слишком сложным для анализа и неотличимо от случайного процесса. Так и происходит, если наблюдать колебания только в одной точке диска Солнца. Однако в процессе анализа наблюдаемого поля колебаний на помощь приходит метод спектрального преобразования - вполне аналогичный разложению в спектр видимого света. Только в гелиосейсмологии такое преобразование выполняется чисто вычислительных образом (без спектрографов), причем последовательно несколько раз. Сначала по отношению к измерениям на видимом диске для каждого момента времени (чтобы выделить разные длины волн), а затем к каждой полученной величине как функции времени.

После такого преобразования пространственно-временного сигнала в спектр колебаний (преобразование называется преобразованием Фурье) оказывается, что спектральная мощность концентрируется около некоторых частот и выделенных значений длин волн. (Такая ситуация вполне аналогична образованию в оптическом спектре фраунгоферовых линий). Другими словами, оказываются возможными (и наблюдаются) только колебания с определенными периодами и длинами волн. Для каждой возможной длины волны допустимые частоты свои, хотя в целом легко найти общие закономерности в последовательностях частот.

Такая картина соответствует математической природе волн. Оказывается, что для описания произвольной волны внутри системы конечных размеров (которой соответствует Солнце в целом) достаточно использовать набор элементарных колебаний, в которых каждая точка системы колеблется строго периодически и в одной фазе. Такие элементарные колебания называют собственными колебаниями (или модами) системы, а совокупность их периодов (частот) и характерных длин волн образует колебательный спектр системы. При определенных условиях (например, конечность системы и адиабатичность колебаний) этот спектр оказывается дискретным - то есть собственные моды возможны только на определенных частотах и длинах волн. Хотя общее количество таких собственных частот бесконечно, но не все из них доступны в наблюдениях.

Собственные моды соответствуют возможному колебанию системы, но их не просто сопоставить с обычной волной. Каждая собственная мода охватывает всю систему сразу, то есть по определению является глобальным колебанием, даже если длина волны мала. Такое колебание не соответствует волне, распространяющейся от источника к следствию. Возбудить колебания в одной чистой моде очень трудно - нужны специальные начальные условия возбуждения сразу во всех точках системы. Но использование преобразования Фурье при обработке нацелено на выделение именно собственным мод, поскольку, во-первых, выделяются чисто периодические колебания, а во-вторых, при обработке используется информация по всему диску сразу и одновременно - как это и предполагается в собственных колебаниях.

Таким образом, первичной целью наблюдательной гелиосейсмологии является высокоточное измерение отдельных собственных частот в возможно большем диапазоне частот и горизонтальных длин волн.

Как наблюдают в гелиосеймологии?

Для того, чтобы выделить собственные колебания, нужно знать геометрические свойства распределения амплитуды колебаний в каждой точке - эта картина распределения амплитуд напоминает стоячую волну, возбуждаемую в натянутой струне. Распределение амплитуд можно описать, задавая положение узлов - множества точек, где амплитуда колебаний равна нулю. В стоячей волне плоскости узлов неподвижны.

Количество узлов часто используют как целый параметр для характеристики отдельных мод колебаний. Число узлов вдоль радиуса называют порядком моды n. Для определения моды с точки зрения поверхностной картины используют два целых числа - степень моды l и азимутальное число m. Эти числа также связаны с количеством узлов по широте и долготе, но более важно, что степень моды l тесно связана с горизонтальной длиной волны. Если степень l достаточно велика, то локально поле колебаний неотличимо от картины плоских волн с длиной волны λ _h = 2π R_⊗/ l;. Моды с очень низкими степенями l трудно сопоставлять с плоскими волнами из-за влияния сферической геометрии поверхности. При l=0 мы имеем просто радиальные колебания, когда амплитуда постоянна на каждой сфере. Все остальные моды называют нерадиальными. При l=1 -- моды называются дипольной, при l=2 квадрупольной. На рис.3 представлены некоторые примеры распределения амплитуд по поверхности для собственных мод.

Современные эксперименты по наблюдениям солнечных колебаний можно разделить на несколько групп, прежде всего по характеру измеряемого сигнала. Наиболее популярны измерения доплеровских скоростей. Поскольку скорость есть величина векторная, то можно говорить только об измерении проекции скорости на луч зрения, то есть несколько неполной информации. Кроме того, с Земли наблюдается только видимая половина полусферы Солнца. Все это создает трудности при выделении сигналов мод с разными l и m в процессе обработки даже при идеальном измерении всего видимого поля колебаний. Разделить колебания мод разных порядков вообще невозможно, так как распределение амплитуд по глубине не наблюдается. Для наблюдателя они отличаются только периодами. В итоге, после анализа пространственной картины, получается сигнал, соответствующий сумме около десятка периодических колебаний (с разнесенными периодами), который и превращают в спектр колебаний для оценки собственных частотою.

Несколько особую группу составляют эксперименты, в которых колебательный сигнал измеряется от всего Солнца в целом. В этом случае обязательно смешиваются моды самых низких степеней (радиальные, дипольные), что создает трудности при идентификации спектра. Для исключения влияния паразитных пиков в спектре, наблюдения в этом случае обязательно должны быть непрерывными, без разрывов на ночь, что достигается либо при последовательных наблюдениях в сети станций, разбросанных по земному шару, либо в космических наблюдениях.

Колебания также можно наблюдать по вариациям яркости - поскольку сжатие элемента газа сопровождается повышением температуры и увеличением яркости. Амплитуды вариаций яркости, связанные с наблюдаемыми колебаниями, очень малы и требуют предельно точной регистрации. В частности, измерение колебательных вариаций яркости от всего Солнца возможно только из космоса, поскольку флуктуации прозрачности земной атмосферы создают слишком большой шум.

Наконец, чтобы получить точную и устойчивую оценку частоты отдельной моды, нужны весьма и весьма длительные ряды наблюдений. Современные требования диктуют необходимость непрерывных наблюдений в течение многих месяцев, или даже лет.

Физика солнечных колебаний

Важнейшим этапом в интерпретации колебаний является выяснение физической природы сил, обеспечивающих возвращение системы в состояние равновесия (возвращающих сил). Одним из способов сделать это является измерение скорости распространения возмущения в среде - так называемой групповой скоростиволн. Для этого в наблюдаемом поле колебаний нужно найти корреляцию колебаний для разных точек на диске в разное время и вычислить запаздывание во времени. После этого вычисленная скорость волны сравнивается с характерными для данной среды скоростями. Если пренебречь наличием магнитных полей, то для газовой среды наиболее существенной является адиабатическая скорость звука - cкорость распространения возмущения в виде областей сжатия или разрежения. Она равна

c_s² = (dP/dρ)_s=(dlnP/dlnρ)_s (P/ρ)

Логарифмическая производная давления по плотности при постоянной энтропии называется показателем адиабатической сжимаемости (Γ₁=(dlnP/dlnρ)_s), и хотя она может меняться в некоторых пределах, но остается близкой к величине 5/3, характерной для идеального одноатомного газа. Для идеального газа скорость звука может быть вычислена через температуру T и молекулярный вес μ

c_s² =(Γ₁P/ρ) = (5/3) (R_gasT/μ)

Уже простые оценки показывают, что наблюдаемые пятиминутные колебания являются в основном акустическими колебаниями, то есть звуковыми волнами (p-моды). Сложность интерпретации колебаний в значительной степени связаны с тем, что параметры среды на Солнце быстро меняются с глубиной. В частности, скорость звука быстро растет с глубиной на Солнце, вместе с температурой.

Акустическая волна может распространяться во всех направлениях вдоль поверхности Солнца и вдоль радиуса. Важным для интерпретации пятиминутных колебаний является то, что звук может относительно свободно распространяться в недрах Солнца, испытывая лишь рефракцию от самых глубоких слоев с очень большой скоростью звука (скорость звука c играет роль показателя преломления для акустических волн). Однако распространение звука вверх за пределы фотосферы оказывается затруднительным из-за очень быстрого падения плотности во внешних слоях. Как следствие, звук оказывается " пойманным " внутри Солнца, отражаясь изнутри от фотосферных слоев.

Таким образом, волновая энергия не может покинуть Солнце через внешние слои и остается в недрах, пока процессы диссипации (лучистое охлаждение более теплых сжатых элементов) и возбуждения других волн не приведут к ее рассеиванию. Из-за значительной непрозрачности вещества в недрах Солнца, диссипация звуковых волн происходит очень и очень медленно, практически незаметно. Отклик от возмущения среды, возникнув, может обежать все Солнце десятки раз (время распространения акустической волны вдоль поверхности около часа, время жизни волны в десятки раз больше), прежде чем его следы исчезнут. Тем самым, даже мелкая рябь волн, наблюдаемых на поверхности, является волновым процессом, охватывающим все Солнце. Разница между короткими и длинными наблюдаемыми на Солнце волнами состоит лишь в направлении вектора распространения волны - мелкомасштабные колебания соответствуют волнам вдоль поверхности, тогда как колебания, охватывающие значительную часть видимого диска, просто соответствуют волнам, уходящим вглубь.

Вопрос о времени жизни волны до ее исчезновения решается на основании вида линий в наблюдаемом спектре мощности. Если изучаемая мода будет бесконечно периодическим колебанием с постоянными периодом и амплитудой, то соответствующая ей линия в спектре будет очень тонкой и высокой. Однако, если процесс состоит из отдельных цугов волн, или затухающих синусоид, или наблюдения проводятся в течение коротких интервалов времени, то спектральные линии будут широкими, причем ширина линии характеризует время жизни отдельной синусоидальной волны. Наблюдаемые на Солнце колебания представляются в спектре мощности линиями шириной около δ ν =1 μHz, тем самым время жизни волны составляет примерно T_wave ≈ 1/δ ν = 10 дней. Именно измерения времени жизни являются основаниями для того, чтобы говорит о глобальности колебаний.

Детальная картина возбуждения и затухания волн, равно как и вопросы об источниках возбуждения значительно более сложны и окончательно не изучены. Известно, что источники акустических волн находятся на глубине около сотни километров под видимыми слоями фотосферы, и связаны со слоями интенсивной конвекции. Возможно, что элементарными источниками являются явления резкого коллапса стекающего вглубь охлажденного газа в так называемых межгранульных промежутках.

Строение солнечных недр по гелиосейсмическим данным.

Гелиосейсмические наблюдения дают нам редкую возможность заглянуть в недра звезды. Основой гелиосейсмологии является гипотеза о взаимности структуры объекта и его спектра. Это означает, что по известной структуре можно вычислить спектр собственных колебаний, но также и обратное - по полному спектру (при дополнительных ограничениях) можно восстановить структуру объекта. На практике данная задача усложняется из-за недостаточности только самих собственных частот и их приближенности, а также из-за ограниченности интервала наблюдаемых частот. В результате, помимо усложнения способов решения задачи, мы должны помнить о принципиальных ограничениях на возможные результаты - нельзя получить то, что нам хочется с произвольной точностью, можно лишь получить "спектрально измеримые" комбинации величин в определенных интервалах и то приближенно.

Несмотря на ограничения, в гелиосейсмологии удалось получить ряд важных результатов. Они прежде всего касаются восстановления скорости звука как функции радиуса в недрах Солнца. Общая идея такого восстановления достаточно проста - если мы можем по наблюдениям вычислить время распространения волны вдоль двух близких путей в недрах Солнца, отличающихся глубиной рефракции, то разность этих времен должна нести информацию о скорости звука в слое, где эти пути отличаются (с учетом необходимых математических поправок на геометрию задачи). Возможности и точность данного восстановления зависят как от точности наблюдательных данных, так и от структуры спектра, поскольку доступные измерениям волновые пути определяются набором собственных мод. В результате скорость звука оказывается известной в диапазоне радиусов от 0.95 до 0.1R_\odot с точностью до 0.1 %. Однако мелкие детали изменения этого профиля по радиусу не могут быть восстановлены таким способом - наша разрешающая способность ограничена диапазоном наблюдаемых периодов колебаний.

Несмотря на это, по восстановленному профилю скорости звука удалось определить положение нижней границы конвективной зоны, где профиль производной скорости звука испытывает излом. Нижняя граница конвекции оказалась на глубине 29 % R_\odot.

В значительной степени аналогичным методом удалось получить информацию о характере внутреннего вращения Солнца, с учетом его зависимости и от глубины и от широты. Влияние вращения на колебания относительно просто представить себе, если использовать представление собственных мод в виде экваториально бегущих, а не стоячих волн. Если собственная мода имеет узлы по экватору (в том и только в том случае, когда m ≠ 0, то сумма двух базисных колебаний m и -m) со смещением на π/2 по времени дают бегущую волну. Другой независимой бегущей волной будет волна, бегущая в обратную сторону. Естественно, что из-за вращения Солнца собственная частота бегущих волн будет смещена на ± ω _rot. Тем самым, спектральная линия для моды с заданными n и l оказывается расщепленной на вращательные компоненты в зависимости от m. Точное значение расщепления зависит от скорости вращения всех слоев, где проходит волна, и сравнивая вращательное расщепление разных мод, можно получить детальную картину внутреннего дифференциального вращения.

Применение значительно более сложных процедур и дополнительных гипотез позволило сделать выводы о содержания гелия во внешних слоях Солнца, что весьма затруднительно сделать другими методами. Оно оказалось 24-25 % содержания по массе, что заметно меньше, чем предполагалось до использования сейсмических методов.

( В редакции Р.Д.И. Стрельцова http://galaxy-science.ru/  по материалам crydee.sai.msu.ru/~vab/Helio.Intro/gelio.htm )